Remember that the formula for a cylinder is:
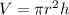
 is the radius of the base (the radius of the circle on top or bottom)
is the radius of the base (the radius of the circle on top or bottom)
 is the height of the cylinder
is the height of the cylinder
In this case, the graph visibly states that the height of the cylinder is 20 cm. However, there is no visibly stated radius. We can thus instead use the diameter of the circle base and divide it by one half (the radius of a circle is one-half of the diameter). Thus, the radius is found as:
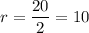
Now, we can insert our values into the formula to find the volume of the shape.
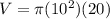
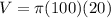
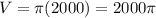
Thus, our answer is Choice B, or 2000π.