Question

Calculate the sum of the infinite series 98+84+72+432/7+...

Answer 1

D. 686

Explanation:

Answer 2

ANSWER


`S_\infty= 686`


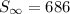
EXPLANATION

The given infinite series is


`98 + 84 + 72 + (432)/(7) + ...`

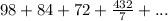
The sum to infinity of this series is given by the formula,


`S_\infty= (a_1)/(1 - r)`

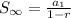
where the first term of this infinite geometric series is


`a_1 = 98`


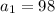
and the common ratio is

`r = (a_2)/(a_1)`



`r = (72)/(98) = (6)/(7)`


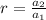
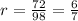
We substitute these values to obtain,



`S_\infty= (98)/(1 - (6)/(7) )`

We simplify the denominator to get,



`S_\infty= (98)/((1)/(7) )`


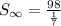
This simplifies to


`S_\infty= 98 * 7 = 686`