Question

PLEASE HELP!!! Trapezoid ABCD was dilated to create trapezoid A'B'C'D'. Which statements are true about the trapezoids? Check all that apply. The length of side AD is 8 units. The length of side A'D' is 4 units. The image is larger than the pre-image. Sides CD and C'D' both have the same slope, 2. The scale factor is .

Answer 1

A, B & E I just took the text

Step-by-step explanation: Ed 2021

Answer 2

Option A , B and D are true.

The statement which are true:

The length of side AD is 4 units

The length of side A'D' is 8 units.

The scale factor is,
`(1)/(2)`

Explanation:

Given in figure trapezoid ABCD;

The coordinates of ABCD are:

A= (-4, 0)

B = (-2, 4)

C = (2,4)

D = (4, 0)

Since, trapezoid ABCD was dilated to create trapezoid A'B'C'D' as shown in figure;

The coordinates of A'B'C'D' are;

A' =(-2, 0)

B'=(-1, 2)

C' = (1, 2)

D' = (2, 0)

First calculate the length of AD

Using Distance formula for any two points i.e,

`√((x_2-x_1)^2+(y_2-y_1)^2)`

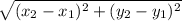
Since, A = (-4, 0) and D = (4, 0)

then;

Length of AD =
`√((4-(-4))^2+(0-0)^2)  = √((4+4)^2) =√(64)=8` units

Therefore, the length of side AD is, 8 units.

Similarly find the length of A'D'.

Where A' = (-2, 0) and D' =(2,0)

Using distance formula:

Length of A'D' =
`√((2-(-2))^2+(0-0)^2) =√((2+2)^2)= √(4^2) = 4`

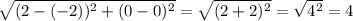
Therefore, the length of side A'D' is, 4 units.

Now, find the slope of CD and C'D'

where C =(2, 4) , D = (4, 0) , C' = (1, 2) and D' =(2,0)

using slope formula for any two points is given by:

`Slope = (y_2-y_1)/(x_2-x_1)`

`Slope of CD = (0-4)/(4-2) = (-4)/(2) = -2`

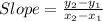
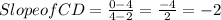
Similarly,

`Slope of C'D' = (0-2)/(2-1) = (-4)/(2) = -2`

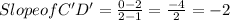
Since, Sides CD and C'D' have same slope i.e, -2

Scale factor(k) states that every coordinate of the original figure has been multiplied by the scale factor.

• If k > 1, then the image is an enlargement.

• if 0<k< 1, then the image is a reduction.

• If k = 1, then the figure and the image are congruent.

The rule for dilation with scale factor(k) is;

`(x, y) \rightarrow (kx , ky)`

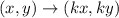
To find the scale factor:

A = (-4, 0) and A' = (-2, 0)

`(-2, 0) \rightarrow (-4k , 0)`

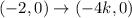
On comparing we ghet;

-4k = -2

Divide -4 both sides we get;

`k = (1)/(2)`

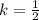
∴ The Scale factor is,
`k = (1)/(2)`

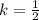
Since, k < 1 which implies the image is a reduction.

Therefore, the statements which are true regarding about trapezoids are;

The length of side AD is 4 units

The length of side A'D' is 8 units.

The scale factor is,
`(1)/(2)`