Question

Given: KPST is a trapezoid, KP=ST, MN is a midsegment, MN=20, h=15, PS:KT=3:7 Find: KS and KP

Answer 1

Length of KS = 25 units

And

Length of KP = 17 units.

Explanation:

Given: KPST is a trapezoid, KP =ST, MN is a mid segment, h is the height =15

Also it is given that, MN = 20 , h = 15 and PS:KT = 3:7.

• If two sides of the trapezoid are equal then, it is an isosceles trapezoid.

• Mid-segment of a trapezoid is a line segment which connects the midpoints of the non-parallel sides.

• A trapezoid mid segment connects the midpoints of two congruent sides of the trapezoid and is parallel to the pair of parallel sides.

• Length of the mid segment is the sum of two bases divide by 2

Since, the length of Mid-segment MN = 20.

Also, it is given: PS:KT = 3:7

Let PS = 3x and KT = 7x respectively.

then;

`(PS+KT)/(2) = 20`

`(3x+7x)/(2) = 20`

`(10x)/(2) =20`

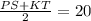
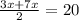
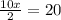
On Simplify, we get;

5x =20

Divide both sides by 5 we get;

x =4

Then:

Length of base PS = 3x = 3(4) = 12 and Length of base KT = 7x = 7(4) = 28.

Now, In triangle PLK

Using Pythagoras theorem to find KP;

It is given here, PL =h =15 and KL= 8 {you can see in the figure as shown below};

`KP^2= PL^2 + KL^2`

`KP^2 = 15^2+8^2 =225 +64 = 289`

`KP = √(289)`

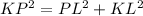
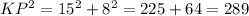
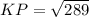
Simplify:

KP = 17

therefore, the length KP = 17 units

To, construct a line: Join K and S

Now, in triangle KRS

KR = KL +LR = 8 +12 =20 and SR = h= 15

Using Pythagoras theorem in KRS to find KS;

`KS^2 = SR^2+KR^2`

`KS^2 = 15^2 + 20^2 = 225 + 400 = 625`

`KS = √(625)`

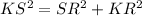
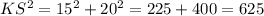
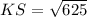
On simplify:

KS = 25

Therefore, the length of KS is, 25 units.