Question

Given: ABCD is a trapezoid, AB=CD, MN is a midsegment, MN=30, BC=17, AB=26 Find: m∠A, m∠B, m∠C, and m∠D

Answer 1

The measures of angle ∠A, ∠B, ∠C, and ∠D are 60, 120, 120 and 60 degree respectively.

Explanation:

Given information:AB=CD, MN is a midsegment, MN=30, BC=17, AB=26

Since two opposites sides are equal, therefore we can say that two no parallel sides are equal.

The length of midsegment is average of length of parallel lines.

`MN=(AD+BC)/(2)`

`30=(AD+17)/(2)`

`60=AD+17`

`43=AD`

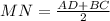
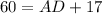
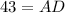
Draw perpendiculars on AD from B and C. Let angle A be θ. D

`AD=AE+EF+FD`

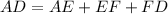
Since ABCD is an isosceles trapezoid, therefore AE=FD and EF=BC

`AD=AE+EF+AE`

`43=2(AE)+17`

`26=2(AE)`

`13=AE`

`\cos\theta=(base)/(hypotenuse)`

`\cos\theta=(AE)/(AB)`

`\cos\theta=(13)/(26)`

`\cos\theta=(1)/(2)`

`\theta=\cos^(-1)(1)/(2)`

`\theta=60`

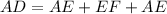
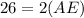
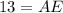
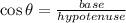
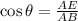
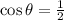
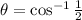
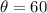
Since ABCD is an isosceles trapezoid, therefore angles A and D are same. Angle B and C are same.

`\angle A=\angle D=60^(\circ)`

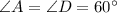
The sum of two consecutive angles of a trapezoid is 180 degree by consecutive interior angle theorem.

`\angle A+\angle B=180^(\circ)`

`60^(\circ)+\angle B=180^(\circ)`

`\angle B=120^(\circ)`

`\angle B=\angle C=120^(\circ)`

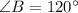
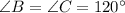
Therefore measures of angle ∠A, ∠B, ∠C, and ∠D are 60, 120, 120 and 60 degree respectively.