Answer:
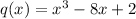

Explanation:
When dividing numbers, we find the quotient or answer by knowing multiplication facts. When 9 is divided by 3, we know that 3x3=9. This 3 is our answer.
When dividing polynomials, we find the quotient by knowing how to multiply expressions. For instance, x(x+1) can be found by multiplying (using the distributive property) x by x to get x squared and then multiplying x by 1 to get x. This gives the expression
 . If I were to divide
. If I were to divide
 by x, my answer would be (x+1) since x(x+1) equals
by x, my answer would be (x+1) since x(x+1) equals
 .
.
Now lets divide
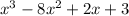 by x. I start by dividing x into the first term.
by x. I start by dividing x into the first term.
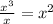 because x times
because x times
 is
is
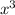 .
.
Next we divide x into the second term.
 .
.
We continue by dividing x into the third term.
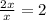
We finish by dividing x into the last term. But because 3 has no variable this can not be done. Nothing times x will give just 3. So r(x) or our remainder will be
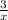 .
.
We put together all the quotients we found by dividing each term and get
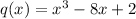 .
.