Question

The perpendicular bisectors of two sides of a triangle meet at point that belongs to the third side. Prove that this is a right triangle.

Answer 1

Statement : If the perpendicular bisectors of two sides of a triangle meet at point that belongs to the third side then this is a right angle triangle.

Prove:

Let ABC is triangle,

In which DF and EF are the perpendicular bisectors of legs AB and BC respectively.

That is, ∠ FDB = ∠BEF= 90°

Where,
`F\in AC`

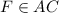
Then By the property of the circumcenter,

F must be mid point of leg AC.

That is, DF ║ BC

⇒ ∠ FDB + ∠ DBC = 180° ( the sum of two adjacent angles on the parallel lines by the same transversal is supplementary )

But, ∠ FDB = 90°

⇒∠ DBC = 90°

⇒ ∠ ABC = 90°

That is, Δ ABC is a right angle triangle.