Question

PLZ HELP I DONT UNDERSTAND

An odd degree power function has a positive leading coefficient.


Which answer correctly describes the function's end behavior?


As x→∞ , f(x)→−∞ (a)

As x→−∞ f(x)→∞


As x→∞ , f(x)→∞ (B)

As x→−∞ , f(x)→−∞


As x→∞ , f(x)→∞ (C)

As x→−∞ , f(x)→∞


As x→∞ , f(x)→−∞

As x→−∞ , f(x)→−∞ (D)

Answer 1

The correct option is B.

Explanation:

If a function is odd degree power function has a positive leading coefficient, then

`f(x)\rightarrow \infty\text{ as }x\rightarrow \infty`

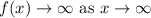
and

`f(x)\rightarrow -\infty\text{ as }x\rightarrow -\infty`

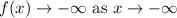
Let an odd degree power function has a positive leading coefficient be

`f(x)=x^3`

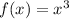
As the value of x increases without bound then the value of f(x) is also increases without bound.

`lim_(x\rightarrow \infty)f(x)=(\infty)^3=\infty`

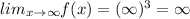
As the value of x decreases without bound then the value of f(x) is also decreases without bound.

`lim_(x\rightarrow -\infty)f(x)=(-\infty)^3=-\infty`

Therefore option B is correct.