Question

Balance the following redox equations. All occur in acid solution. (Type your answer using the format CO2 for CO2 and [NH4] for NH4 . Use the lowest possible coefficients.) (a) MnO4-(aq) (aq) HSO3-(aq) Mn2 (aq) (l) SO42-(aq)

Answer 1

`H^++2(Mn^(7+)O_4)^- +5(HS^(+4)O_3)^-\rightarrow 2Mn^(2+)+ 3H_2O+5(S^(6+)O_4)^(2-)`

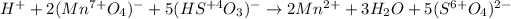
Step-by-step explanation:

Hello!

In this case, according to the given problem, we need to balance the following redox chemical equation in acidic solution:

`(MnO_4)^-+HSO_3^-\rightarrow Mn^(2+)+(SO_4)^(2-)`

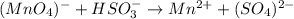
Thus, the first step is to assign the oxidation states for both manganese and sulfur as that of oxygen is not changing from 2-:

`(Mn^(7+)O_4)^-+HS^(+4)O_3^-\rightarrow Mn^(2+)+(S^(6+)O_4)^(2-)`

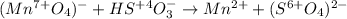
Now, we realize that manganese is undergoing reduction from 7+ to 2+ and sulfur is undergoing oxidation from 4+ to 6+, so we write the half-reactions:

`(Mn^(7+)O_4)^-\rightarrow Mn^(2+)\\\\HS^(+4)O_3^-\rightarrow (S^(6+)O_4)^(2-)`

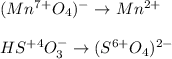
Next we insert the transferred electrons and the necessary hydrogen ions and water molecules to balance the half-reactions:

`8H^++(Mn^(7+)O_4)^-+5e^-\rightarrow Mn^(2+)+4H_2O\\\\(HS^(+4)O_3)^-+H_2O\rightarrow (S^(6+)O_4)^(2-)+3H^++2e^-`

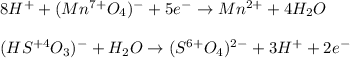
Then, we cross multiply the transferred electrons:

`2(8H^++(Mn^(7+)O_4)^-+5e^-\rightarrow Mn^(2+)+4H_2O)\\\\5[(HS^(+4)O_3)^-+H_2O\rightarrow (S^(6+)O_4)^(2-)+3H^++2e^-]\\\\\\16H^++2(Mn^(7+)O_4)^-+10e^-\rightarrow 2Mn^(2+)+8H_2O\\\\5(HS^(+4)O_3)^-+5H_2O\rightarrow 5(S^(6+)O_4)^(2-)+15H^++10e^-`

And we can add them up in the form of the initial reaction, by making sure we cancel out the transferred electrons at both sides and simply the common hydrogen ions and water molecules at both sides also:

`16H^++2(Mn^(7+)O_4)^-+10e^-+5(HS^(+4)O_3)^-+5H_2O\rightarrow 2Mn^(2+)+8H_2O+5(S^(6+)O_4)^(2-)+15H^++10e^-\\\\16H^++2(Mn^(7+)O_4)^- +5(HS^(+4)O_3)^-+5H_2O\rightarrow 2Mn^(2+)+8H_2O+5(S^(6+)O_4)^(2-)+15H^+\\`

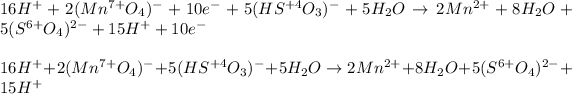
Finally, the result is:

`H^++2(Mn^(7+)O_4)^- +5(HS^(+4)O_3)^-\rightarrow 2Mn^(2+)+ 3H_2O+5(S^(6+)O_4)^(2-)`

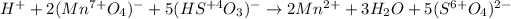
Best regards!