Question

How is the graph of y=-1/3x related to its parent function y=1/x

A. It is horizontally stretched by a factor of 3 and reflected over the x-axis.
B. It is horizontally stretched by a factor of 3 and reflected over the y-axis.
C. It is horizontally compressed by a factor of 3 and reflected over the x-axis.
D. It is horizontally compressed by a factor of 3 and reflected over the y-axis.

Answer 1

Answer: OPTION C.

Explanation:

Some tranformations for a function f(x):

If
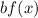`bf(x)`, and
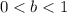`0<b<1`, then the function is vertically compressed by a factor of "b".

If
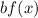`bf(x)`, and
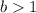`b>1`, then the function is vertically stretched by a factor of "b".

If
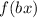`f(bx)`, and
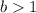`b>1`, then the function is horizontally compressed by a factor of "b".

If
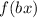`f(bx)`, and
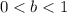`0<b<1`, then the function is horizontally stretched by a factor of "b"

If
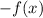`-f(x)`, then the function is reflected over the x-axis.

If
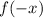`f(-x)`, then the function is reflected over the y-axis.

Given the function
`y=-(1)/(3x)` and the parent function
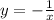`y=-(1)/(x)`, you can observe that:

The function
`y=-(1)/(3x)` is the function
`y=(1)/(x)` but horizontally compressed by a factor of 3 and reflected over the x-axis.