Question

Which of the following quartic functions has x=-1 and x=-3 as its only two real zeros

A.y=x^4-4x^3-4x^2-4x-3
B.y=-x^4-4x^3+4x^2+4x+3
C.y=x^4+4x^3+3x^2+4x-4
D.y=x^4+4x^3+4x^2+4x+3

Answer 1

option D

Explanation:

x=-1 and x=-3 are the real zeros

We plug in the x values in each equation and check which equation makes y=0

A) y=x^4-4x^3-4x^2-4x-3

x=-1 ,
`y=(-1)^4-4(-1)^3-4(-1)^2-4(-1)-3= 2`

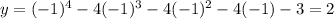
x=-3 ,
`y=(-3)^4-4(-3)^3-4(-3)^2-4(-3)-3= 162`

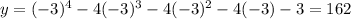
y is not equal to 0 so option A is not correct

B.y=-x^4-4x^3+4x^2+4x+3

x=-1 ,
`y=(-1)^4-4(-1)^3+4(-1)^2+4(-1)+3=6`

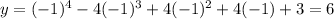
x=-3 ,
`y=(-3)^4-4(-3)^3+4(-3)^2+4(-3)+3=54`

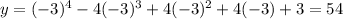
y is not equal to 0 so option B is not correct

C.y=x^4+4x^3+3x^2+4x-4

x=-1 ,
`y=(-1)^4+4(-1)^3+4(-1)^2+4(-1)-4= -8`

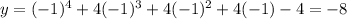
x=-3 ,
`y=(-3)^4+4(-3)^3+4(-3)^2+4(-3)-4= -16`

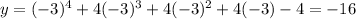
y is not equal to 0 so option C is not correct

D) y=x^4+4x^3+4x^2+4x+3

x=-1 ,
`y=(-1)^4+4(-1)^3+4(-1)^2+4(-1)+3= 0`

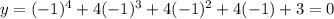
x=-3 ,
`y=(-3)^4+4(-3)^3+4(-3)^2+4(-3)+3= 0`

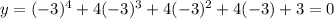
y=0 so option D has two real zeros x=-1 and x=-3