Question

Krissy wanted to understand whether grade level had any relationship to their opinion on extending the school day. She surveyed some students and displayed the results in the table below:

In favor Opposed Undecided
Grade 9 6 2 7
Grade 10 5 11 8
Grade 11 12 15 11
Grade 12 17 5 13


Compare P(Grade 11 | opposed) with P(opposed | Grade 11).

Answer 1

c

Explanation:

Answer 2

P(Grade 11 | opposed) =0.4545

P(opposed | Grade 11)=0.3947

Explanation:

The table displaying the data is given below as:

In favor Opposed Undecided Total

Grade 9 6 2 7 15

Grade 10 5 11 8 24

Grade 11 12 15 11 38

Grade 12 17 5 13 35

Total 40 33 39 112

Now we are asked to compare the conditional probability i.e. we are asked to compare P(Grade 11 | opposed) with P(opposed | Grade 11).

let A denote the event that the student is in grade 11.

and B denote the event of opposing the decision.

Then A∩B denote the event of grade 11 students who opposed.

Hence, we are asked to compare:

P(A|B) and P(B|A)

We know that:

`P(A|B)=(P(A\bigcap B))/(P(B))\\\\and\\\\P(B|A)=(P(A\bigcap B))/(P(A))`

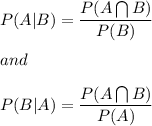
Now from the table we have:

P(A)=38/112

P(B)=33/112

P(A∩B)=15/112

Hence,

`P(A|B)=((15)/(112))/((33)/(112))\\\\\\P(A|B)=(15)/(33)=0.4545`

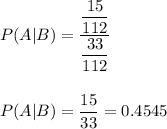
Similarly:

`P(B|A)=((15)/(112))/((38)/(112))\\\\\\P(B\A)=(15)/(38)=0.3947`

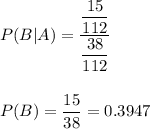
Hence,

P(Grade 11 | opposed) =0.4545

P(opposed | Grade 11)=0.3947