Question

8x+5y=-13
3x+4y=10
what is the x and y using elimination?

Answer 1

`\begin{cases}8x+5y=-13\\3x+4y=10\end{cases}`

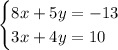
Multiply both equations by appropriate constants to get the coefficients of either
`x` or
`y` in both equations to be the same. One choice would be to multiply the first equation by 3 and the second by 8:

`\begin{cases}24x+15y=-39\\24x+32y=80\end{cases}`

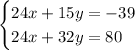
Then subtract either equation from the other to eliminate
`x`. I'll take the first from the second:

`(24x+32y)-(24x+15y)=80-(-39)\implies17y=119\implies y=7`

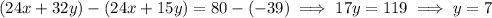
Then solve for
`x` in either equation. From the second one, we find

`3x+4(7)=10\implies3x=10-28=-18\implies x=-6`

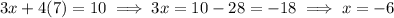
So the solution to this system is the coordinate pair (-6, 7).