Answer:
Hyperbola
Explanation:
The general second degree equation can be written as:
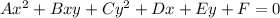
To identify the graph by inspection of equation, then complete any squares if necessary so that the variables are on one side and the constant is on the either right hand side of the equation.
1. Line : Squared term of neither variable is present.
2.Circle :Squared terms of both variables are present, both are positive and both have the same coefficient. The right hand side is positive.
3.Ellipse :Squared terms of both variables are present, both are positive and both have different coefficients. The right hand side is always positive.
4.Parabola :Both variables are present but only one is squared.
5.Hyperbola :Squared terms of both variables are present, but one is positive and the other one is negative. The right hand side is not zero.
For 3, 4 and 5, The general equation reduces to
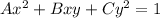
which is a hyperbola if
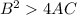 and an ellipse if
and an ellipse if
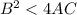 and a parabola if
and a parabola if
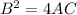 .
.
For the given equation xy=4, we observe that
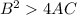 , hence the given equation is an hyperbola.
, hence the given equation is an hyperbola.