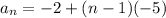Answer:
Option A is correct
General rule for arithmetic sequence with
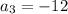 and
and
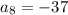 is;
is;
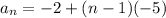
Explanation:
Arithmetic sequence states that a sequence where the difference between each successive pair of terms is the same.
The general rule for the arithmetic sequence is given by;
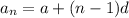 where
where
a represents the first term
d represents the common difference and
n represents the number of terms.
Given:
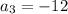 and
and
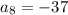
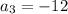
a+(3-1)d = -12 [Using arithmetic sequence rule]
a + 2d = -12
or we can write this as;
a = -12 - 2d ......[1]
Similarly, for
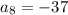 we have;
we have;
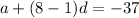
a+7d = -37 ......[2]
Substitute equation [1] into [2] to solve for d;
-12 - 2d +7d = -37
Combine like terms;
-12 + 5d = -37
Add both sides 12 we get;
-12 + 5d + 12 = -37 + 12
Simplify:
5d = -25
Divide both sides by 5 we get;
d = -5
Substitute the value of d in equation [1] to solve for a;
a = -2(-5) - 12
a = 10 -12 = -2
∴ a = -2
therefore, the general rule for the arithmetic sequence with
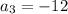 and
and
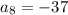 is,
is,