Question

A scalene triangle has the lengths 6, 11, and 12. Keyla uses the law of cosines to find the measure of the largest angle. Complete her work and find the measure of angle Y to the nearest degree.

1. 122 = 112 + 62 − 2(11)(6)cos(Y)
2. 144 = 121 + 36 − (132)cos(Y)
3. 144 = 157 − (132)cos(Y)
4. −13 = −(132)cos(Y)

_____ degrees

Answer 1

84 degrees

Explanation:

Applying the Cosine Rule (Choice 2 is the correct one) :-

12^2 = 11^2 + 6^2 - 2*11*6 cos Y

144 = 121 + 36 - 132 cos Y

cos Y = (121 + 36 - 144) / 132

cos Y = 0.09848

Y = 84.3 degrees

Answer 2

The measure of angle Y is 84°.

Explanation:

The side of a triangle are 6, 11, and 12.

Keyla uses the law of cosines to find the measure of the largest angle.

Law of cosine:

`a^2=b^2+c^2-2bc\cos A`

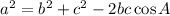
where, a,b, c are sides and A is angle.

Let a=12, b=11, c=6 and angle A=\angle Y

Using law of cosine, we get

`(12)^2=(11)^2+(6)^2-2(11)(6)\cos Y`

`144=121+36-132\cos Y`

`144=157-132\cos Y`

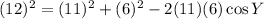
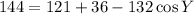
Subtract 157 from both sides.

`144-157=-132\cos Y`

`-13=-132\cos Y`

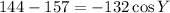
Divide both sides -132.

`(-13)/(-132)=\cos Y`

`(13)/(132)=\cos Y`

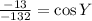
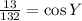
Taking cos⁻¹ both sides.

`\cos ^(-1)(13)/(132)=Y`

`Y\approx 84.348`

`Y\approx 84^(\circ)`

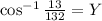
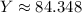
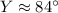
Therefore the measure of angle Y is 84°.