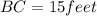Question

Lisa is repairing fences on a piece of ranch land. She needs to arrive at point A from point B in the diagram. But the land there is low and sometimes floods. Before she decides to risk it, she wants to know how much distance she’ll save if she goes straight from B to A instead of taking the dry path from B to C to A. Angle BCA is a right angle. AC = BC + 21 feet, and AB = BC + 24 feet. a triangle diagram representing Lisa's path If Lisa travels straight from B to A, she’ll walk feet, which will save her feet compared with traveling the longer, drier path.

Answer 1

Correction from my spelling,

If she walks from A to C to B*

If you have any question upon my solution, please ask !

Hope this helps you :)

Answer 2

Explanation:

In this problem, you need to apply the Pythagorean theorem because you know this is a right triangle. The path from B to C to A is a right angle.

`AB^(2)=BC^(2)+AC^(2)`

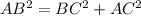
The only unknown is going to be BC, you can arrange again this

`BC^(2)=AC^(2) - AB^(2)`

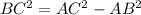
and change the values

`BC^(2) =(BC + 21feet)^(2) - (BC + 24feet) ^(2)`

`BC^(2) =(BC^(2) +2*21feet*BC+21^(2)feet) +( BC^(2) +2*24feet*BC +24^(2)feet)`

`BC^(2)=6BC+476-441\\BC^(2)=6BC+135\\BC^(2)-6BC-135=0`

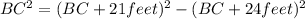
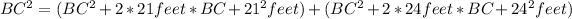
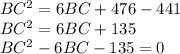
and apply Bhaskara rule

`BC=15`

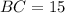
Now you can come back and know all the lengths

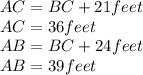`AC=BC+21feet\\AC=36feet\\AB=BC+24feet\\AB=39feet`\\
`BC=15feet`