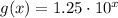Question

Let f(x)=10x

What function represents a transformation of f(x) by a vertical stretch with factor 1.25?

A. g(x)=1.25⋅10^x
B. x)=10^0.8x
C. g(x)=10^1.25x
D. g(x)=0.8⋅10^x

Answer 1

Option A is correct.

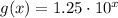`g(x)=1.25 \cdot 10^x` is a function represents a transformation of f(x) by a vertical stretch with factor of 1.25.

Explanation:

Given the function:
`f(x) = 10^x`

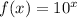
For a base function f(x) and a constant k > 0, the function is given by:

g(x) = kf(x), can be sketched by vertically stretching f(x) by a factor of k

if k>1.

Since, factor(k) = 1.25 > 1.

then;

`g(x) = 1.25 f(x)` .......[1]

Substitute
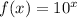`f(x) = 10^x` in [1];

`g(x)=1.25 \cdot 10^x`

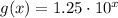
Therefore, the function represents a transformation of f(x) by a vertical stretch with factor 1.25 is,
`g(x)=1.25 \cdot 10^x`