Answer:
Part 1)

Part 2)
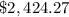
Part 3)
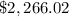
Part 4) In the procedure
Explanation:
Part 1) we know that
The compound interest formula is equal to
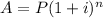
where
A is the Final Investment Value
P is the Principal amount of money to be invested
i is the interest rate in decimal
n is number of years
n is the number of times interest is compounded per year
in this problem we have
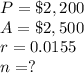
substitute in the formula above

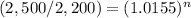
Applying log both sides
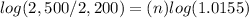
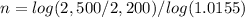
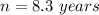
Part 2)
in this problem we have
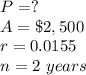
substitute in the formula above

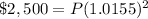
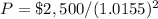

Part 3) in this problem we have
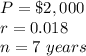
substitute in the formula above
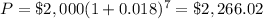
The money is not enough
Part 4)
I would personally increase the investment from 2,200 dollars so that it grows to 2,500 dollars at the time I want to make the trip, for example if I wanted to make the trip in two years, I would increase the initial investment from 2200 dollars to 2427 dollars.