Question

Prove that two right triangles are congruent if a leg and the altitude to hypotenuse of one of the triangles are respectively congruent to a leg and the altitude to the hypotenuse of the other triangle.

Answer 1

Theorem: Two right triangles that have a congruent hypotenuse and a corresponding, congruent leg are congruent triangles.

Prove: Let ABC and DEF are the two right triangles. ( shown in below diagram)

Such that, AB =DE, AC = DF and ∠ABC = ∠ DEF = 90°

Prove: Δ ABC ≅ Δ DEF

Since, In Δ ABC,

`AC^2 = AB^2 + BC^2` ( by Pythagoras theorem)

`AC = √(AB^2 + BC^2)`

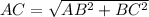
Similarly, In triangle DEF,

`DF = √(DE^2 + EF^2)`

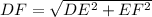
But, AC= DF ( given)

Therefore,
`√(AB^2 + BC^2)= √(DE^2 + EF^2)`

⇒
`AB^2 + BC^2= DE^2 + EF^2`

⇒
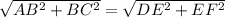
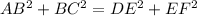
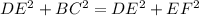`DE^2 + BC^2=DE^2 + EF^2` ( AB= DE)

⇒
`BC^2= EF^2`

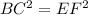
⇒ BC= EF

Therefore, By SSS postulate of congruent,

Δ ABC ≅ Δ DEF