Question

The half life of Pb-210 is 22 years. A decayed animal shows 16% of the original Pb-210 remains; how long has the animal been deceased to the nearest tenth of a year?

58.2 years


58.0 years


0.1 years


0.12 years

Answer 1

The correct option is: 58.2 years.

Explanation:

The half-life formula is:
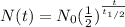`N(t)= N_(0)((1)/(2))^(t)/(t_(1/2))` , where
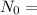`N_(0)=` Original amount,
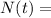`N(t)=` Final amount after
`t` years and
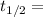`t_(1/2)=` Half-life in years.

The half life of Pb-210 is 22 years. So,
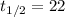`t_(1/2)= 22` years.

A decayed animal shows 16% of the original Pb-210 remains. That means, if
`N_(0)=100`, then
`N(t)= 16`.

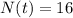Plugging these values into the above formula, we will get......

`16= 100((1)/(2))^(t)/(22)\\ \\ (16)/(100)= (100((1)/(2))^(t)/(22))/(100)\\ \\ 0.16=((1)/(2))^(t)/(22)`

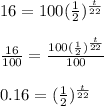
Taking logarithm on both sides.......

`log(0.16)=log[((1)/(2))^(t)/(22)]\\ \\ log(0.16)=(t)/(22)log((1)/(2))\\ \\ (t)/(22)=(log(0.16))/(log((1)/(2)))\\ \\ t= 22*(log(0.16))/(log((1)/(2)))=58.1648... \approx 58.2`

(Rounded to the nearest tenth)

So, the animal has been deceased for 58.2 years.