Question

What's the total mechanical energy of a 300 kg satellite in circular orbit 1500 km above earth's surface?

Answer 1

The mechanical energy of the satellite is about 12 Gigajoules

Step-by-step explanation:

The total mechanical energy is the sum of the kinetic and potential energy:

`E = E_k+E_p\\E = (1)/(2)mv^2+ mgh`

While we can determine the potential energy from the given values (height above earth's surface), to calculate the kinetic energy the velocity of the satellite needs to be determined first.

The formula for orbital velocity is:

`v = \sqrt {(G\cdot m_E)/(r)}`

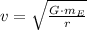
with G the gravitational constant, m_E the mass of the Earth, and r the satellite distance measured from the center of the Earth:

`v = \sqrt{(6.673\cdot10^(-11) Nm^2/kg^2\cdot 5.98 \cdot 10^(24) kg)/(6.38 \cdot 10^6 m+ 1.5\cdot 10^6m)}=7116.20 (m)/(s)`

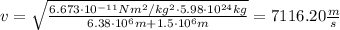
This velocity points in the direction of the tangent of the orbit.

Now the kinetic and total mechanical energy can be calculated:

`E_k+E_p= (1)/(2)mv^2+ mgh=\\=(1)/(2)300kg\cdot 7116.2^2(m^2)/(s^2)+ 300kg\cdot9.8(m)/(s^2)\cdot 1.5\cdot 10^6m= \\= 12006045366J\approx12 GJ`

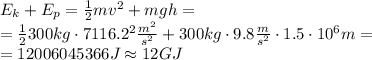
The mechanical energy of the satellite is about 12 Gigajoules