If z=-1-sq root 3i and z^6=a+bi then a = _ and b= _

Question

asked Sep 27, 2019 14.6k views

1 Answer

Caroline Morris · Answer 1 · 2019-10-04T05:18:52+0000

Answer:

a=64 and b=0

Explanation:

z=-1-√(3)i

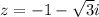
use
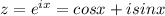
z=e^(ix)=cosx+isinx

Now we find out x using given z

z=-1-√(3)i

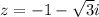
Multiply and divide the right side by -2

z=-2((1)/(2) +(√(3))/(2))

We know cos(pi/3) = 1/2

sin(pi/3)= sqrt(3)/2

z=-2((1)/(2) +(√(3))/(2))

$z=-2(cos((\pi)/(3))+sin((\pi)/(3))$

compare the above equation with use
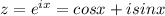
z=e^(ix)=cosx+isinx

x= pi/3

so
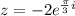
$z=-2e^{(\pi)/(3)i}$

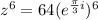
$z^6=64(e^{(\pi)/(3)i})^6$

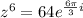
$z^6=64e^{(6\pi)/(3)i}$

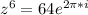
$z^6=64e^(2\pi*i)$

Plug in 2pi in the z equation

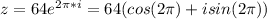
$z=64e^(2\pi*i)=64(cos(2\pi)+isin(2\pi))$

So z= 64(1 + i(0))

z=64

So a= 64 and b=0