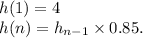Answer:
Explicit formula is
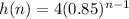 .
.
Recursive formula is
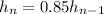
Explanation:
Step 1
In this step we first find the explicit formula for the height of the ball.To find the explicit formula we use the fact that the bounces form a geometric sequence. A geometric sequence has the general formula ,
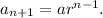 In this case the first term
In this case the first term
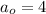 , the common ratio
, the common ratio
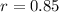 since the ball bounces back to 0.85 of it's previous height.
since the ball bounces back to 0.85 of it's previous height.
We can write the explicit formula as,
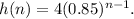
Step 2
In this step we find the recursive formula for the height of the ball after each bounce. Since the ball bounces to 0.85 percent of it's previous height, we know that to get the next term in the sequence, we have to multiply the previous term by the common ratio. The general fomula for a geometric sequene is
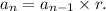
With the parameters given in this problem, we write the general term of the sequence as ,