Question

What is the equation of the line, in slope-intercept form, that is perpendicular to the line with the equation y=6x−1 and passes through the point (−6,4)?

Answer 1

Greetings!

Answer:

y =
`(-x)/(6) + (28)/(6)`

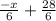
Explanation:

First, we must find the slope of the current equation.

This is the number in front of the x.

Seeing as this is 6x, the slope of this line is 6

When finding the slope of a line perpendicular, you need to find the
`(-1)/(slope)`

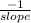
So, in this case it is:

`(-1)/(6)`

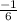
The negatives cancel out which leave
`(1)/(2)`

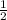
So the gradient is
`(1)/(2)`

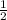
Now, to find the equation of a line, you need to use:

y - y1 = m(x - x1)

Where y1 and x1 are the values in the coordinates (-6 , 4)

So y1 = 4, x1 = -6, and m is
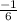`(-1)/(6)`. Plug these values in:

y - 4 =
`(-1)/(6)(x - -6)`

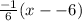
We need to get rid of the fraction so we multiply the whole equation by 6 (6 * 1/6 = 1):

6y - 24 = - (x - 2)

The minus outside the bracket means that every value inside the bracket is oposite:

6y - 24 = -x + 2

And now simply move the -24 over to the other side, making it a positive:

6y = -x +2 + 26

Simplify:

6y = -x + 28

Divide all values by 6 to get y:

y =
`(-x)/(6) + (28)/(6)`

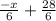
So the equation of the line is y =
`(-x)/(6) + (28)/(6)`

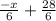
Hope this helps!