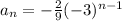Question

Which formula can be used to find the nth term of the following geometric sequence? − 2/9 , 2/3 , −2, 6,…

Answer 1

The formula to find the nth term of a geometric sequence is an = a1 * r(n-1). In the given sequence, the formula would be an = (-2/9) * (2/3)(n-1).

Step-by-step explanation:

The formula to find the nth term of a geometric sequence is:

an = a1 * r(n-1)

Where:

• an is the nth term
• a1 is the first term
• r is the common ratio
• n is the number of terms

In the given sequence, the first term (a1) is -2/9 and the common ratio (r) is 2/3. Therefore, the formula to find the nth term is:

an = (-2/9) * (2/3)(n-1)

Answer 2

`a_n=-(2)/(9)(-3)^(n-1)`

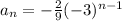
Step-by-step explanation:

Since, the nth term of a geometric sequence is,

`a_n=ar^(n-1)`

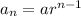
Where, a is the first term of the sequence,

r is the common ratio,

Here, the given geometric sequence is,

`-(2)/(9),(2)/(3),-2,6........`

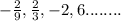
Thus, the first term of the sequence is,

`a=-(2)/(9)`

And, the common ratio,

`r=(2/3)/(-2/9)=-3`

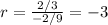
Hence, the nth term of the sequence is,

`a_n=-(2)/(9)(-3)^(n-1)`