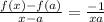Answer:
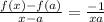
Explanation:
Given
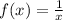
Required
Evaluate
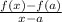
We have:
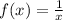
Next, we calculate f(a)
Substitute a for x in
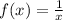
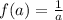
Substitute values for f(x) and f(a) in
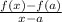
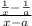
Take LCM of the numerator
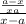
Split:
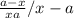
Convert / to *

Express a - x as -(x-a)
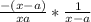
Divide numerator and denominator by x - a
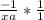
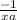
Hence: