Question

Which geometric series converges?

Answer 1

Option D.

Explanation:

For convergence or divergence of any series we should always remember

If common ratio of the terms of the geometric series r > 1 then series Diverges, for r < 1 series converges and for r = 1 series may converge or may diverge.

Now we take each series given in the figure attached

A. common ratio =
`((1)/(6) )/((1)/(6))=1`

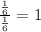
So series may converge or diverge.

B. common ratio =
`((2)/(6))/((1)/(6))=2`

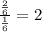
Therefore, r > 1 series will diverge.

C. common ratio =
`(12)/(6)=2`

So r > 1, series will diverge.

D. common ratio =
`(2)/(6)=(1)/(3)`

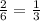
r < 1 therefore, series will converge.

Option D. is the correct option.