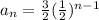Question

Enter the explicit rule for the geometric sequence.

3/2, 3/4, 3/8, 3/16, 3/32, …


a(n)=

Answer 1

ANSWER

The explicit formula is

`a_n= (3)/(2) ({ (1)/(2) })^(n - 1)`


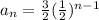
Step-by-step explanation

The given geometric sequence is

`(3)/(2), (3)/(4), (3)/(8), (3)/(16), (3)/(32)`

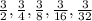
The explicit formula is given by,


`a_n = a_1 ({r})^(n - 1)`


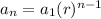
where the first term is

`a_1 = (3)/(2)`


and the common ratio is


`r = (a_2)/(a_1)`


`r = ( (3)/(4) )/( (3)/(2) )`


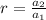
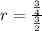
This implies that,



`r = (3)/(4) * (2)/(3)`



`r = (1)/(2)`


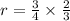
We now substitute all these values in to the formula to obtain,





`a_n= (3)/(2) ({ (1)/(2) })^(n - 1)`