Question

Suppose you invest 1600 at annual interest rate of 7.9% compounded cont how much will u have after 10yrs

35254.34
3525.43
3435.91
17315.27

Answer 1

B. $3525.43

Step-by-step explanation:

We will use continuously compound interest formula to solve our problem.

`A=P*e^(rT)`

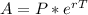
A= Amount after T years.

P= Principal amount.

r= Interest rate (in decimal form).

e= The mathematical constant e.

T= Time in years.

First of all we will convert our interest rate in decimal form.

`7.9\text{ Percent}=(7.9)/(100)=0.079`

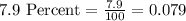
Now let us substitute our given values in above formula.

`A=1600*e^(0.079*10)`

`A=1600*e^(0.79)`

`A=1600*2.2033964262559365`

`A=3525.4342820094984\approx 3525.43`

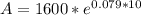
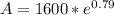
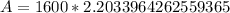
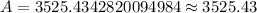
Therefore, we will get an amount of $3525.43 after 10 years and option B is the correct choice.