Answer:
Yes, we can find a unique price for an apple and an orange.
Explanation:
Let x be the price of one apple and y be the price of one orange.
We have been given that a fruit stand has to decide what to charge for their produce. They need $5.30 for 1 apple and 1 orange.
We can represent this information in an equation as:
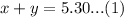
They also need $7.30 for 1 apple and 2 oranges.
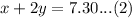
Upon substituting our given information we formed a system of equations. Let us see if this system is solvable or not.
For a unique solution
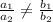 , where
, where
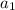 and
and
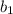 are constant of x and y variables of 1st equation respectively.
are constant of x and y variables of 1st equation respectively.
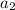 and
and
 are constant of x and y variables of 2nd equation respectively.
are constant of x and y variables of 2nd equation respectively.
Let us check our system of equations for unique solution.
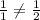

We can clearly see that 1 is not equal to half, therefore, we can find a unique price for an apple and orange using our system of equations.
Upon subtracting our 1st equation from 2nd equation we will get,


Therefore, price of one orange is $2.
Upon substituting y=2 in equation 1 we will get,
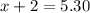
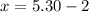
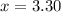
Therefore, price of one apple is $3.30.