Answer:
The value that is greater than 45% of the data values is approximately 137.84.
Explanation:
The key is transforming values from this distribution to a z-score range and finding the corresponding value using a z-score table.
We are looking for a value x which attains a critical z-score that corresponds to the (100-45)%=55-th percentile:

The critical z value (from z-score table, online) is: -0.12, so:
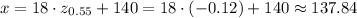
The value that is greater than 45% of the data values is approximately 137.84.