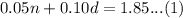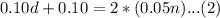Question

A collection of nickels and dimes has a value of 1.85. The value of the dimes is 0.10 less than twice the value of the nickels. Which system of equations can be used to find the number of nickels and the number of dimes

Answer 1

To find the number of nickels and dimes in a collection that totals $1.85, where the value of the dimes is $0.10 less than twice the value of the nickels, we must set up a system of equations: 5n + 10d = 185 and 10d = 2(5n) - 10.

Step-by-step explanation:

The question concerns a system of equations required to solve a problem involving nickels and dimes.

Let n be the number of nickels and d be the number of dimes. Since each nickel is worth 5 cents and each dime is worth 10 cents, we can come up with two equations.

The total value equation is:

• 5n + 10d = 185 (since the total value is $1.85, which is 185 cents)

The value relationship between dimes and nickels is given by:

• 10d = 2(5n) - 10

By solving this system of equations, the number of nickels (n) and dimes (d) can be determined.

Answer 2

Step-by-step explanation:

Let n be the number of nickels and d be number of dimes.

Since we know that the value of one dime equals $0.10 and value of 1 nickel is $0.05, therefore, value of n nickels will be 0.05n and value of d dimes will be 0.10d.

We have been given that a collection of nickels and dimes has a value of 1.85.

Let us represent this information in an equation.

`0.05n+0.10d=1.85...(1)`

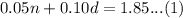
We have been given that the value of the dimes is 0.10 less than twice the value of the nickels.

We can represent this information in an equation as:

`0.10d+0.10=2*(0.05n)...(2)`

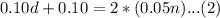
Therefore, our system of equations that can be used to find the number of nickels and the number of dimes is:

`0.05n+0.10d=1.85...(1)`

`0.10d+0.10=2*(0.05n)...(2)`