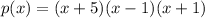Answer:
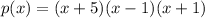
Explanation:
we are given polynomial as
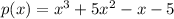
We can group first two terms and last two terms
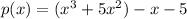
We can factor out -1 from last two terms
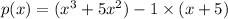
We can see that x^2 is common in first two terms
so, we can factor out x^2 from first two terms
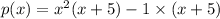
we can see x+5 is in both terms
so, we can factor out x+5
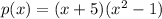
we can also factor it as