Question

An automobile manufacturer claims that its van has a 27.6 miles/gallon (MPG) rating. An independent testing firm has been contracted to test the MPG for this van since it is believed that the van has an incorrect manufacturer's MPG rating. After testing 210 vans, they found a mean MPG of 28.0. Assume the standard deviation is known to be 2.3. A level of significance of 0.05 will be used. State the hypotheses.

Answer 1

Null Hypothesis: H₀: There is no difference between the sample mean and Population mean

H₀ : x⁻ = μ

Test statistic

Z = 2.5204 > 1.96 at 0.05 level of significance

The null hypothesis is rejected at 0.05 level of significance

There is a difference between the sample mean and Population mean

Explanation:

Step(i):-

Given mean of the Population = 27.6 miles/gallon

Sample size 'n' = 210

Mean of the sample = 28.0 miles/gallon

Given the standard deviation of the population = 2.3

Level of significance = 0.05

The critical value Z₀.₀₅ = 1.96

Step(ii):-

Null Hypothesis: H₀: There is no difference between the sample mean and Population mean

H₀ : x⁻ = μ

Alternative Hypothesis:H₁: There is a difference between the sample mean and Population mean

H₁: x⁻ ≠ μ

Test statistic

`Z = (x^(-)-mean )/((S.D)/(√(n) ) ) = (28.0-27.6)/((2.3)/(√(210) ) )`

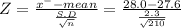
Z = 2.5204

Z = 2.5204 > 1.96 at 0.05 level of significance

The null hypothesis is rejected at 0.05 level of significance

There is a difference between the sample mean and Population mean