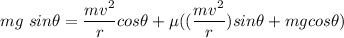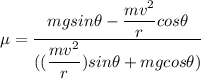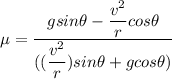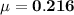Question

If a car takes a banked curve at less than the ideal speed, friction is needed to keep it from sliding toward the inside of the curve (a real problem on icy mountain roads). (a) Calculate the ideal speed to take a 100 m radius curve banked at 15.0o. (b) What is the minimum coefficient of friction needed for a frightened dri

Answer 1

a) The ideal speed = 16.21 m/s

b) Minimum co-efficient of friction = 0.216

Step-by-step explanation:

From the given information:

The ideal speed can be determined by considering the centrifugal force component and the gravity component.

`(mv^2)/(r)cos \theta = mg sin \theta`

`v = \sqrt {gr \ tan \theta}`

`= √((9.8 \ m/s^2) (100) \ tan 15^0)`

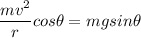
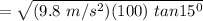
= 16.21 m/s

(b)

Let assume that it requires 25 km/h to take the same curve.

Then, using the equilibrium conditions;

`mg \ sin \theta = (mv^2)/(r) cos \theta + \mu (((mv^2)/(r)) sin \theta + mg cos \theta)`

`\mu = (mg sin \theta - (mv^2)/(r) cos \theta )/((((mv^2)/(r)) sin \theta + mg cos \theta) )`

`\mu = (g sin \theta - ( v^2)/(r) cos \theta )/((((v^2)/(r)) sin \theta + g cos \theta) )`

`\mu = ((9.8 \ m/s^2 ) sin (15^0) - ( ((25 * 10^3)/(3600) \ m/s)^2 )/(100 \ m ) cos (15^0) )/((((((25 * 10^3)/(3600) )^2)/(100)) sin 15^0 + (9.8 \ m/s^2) cos 15^0 ) )`

`\mathbf{\mu = 0.216}`