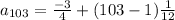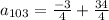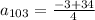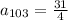Question

What is the 103rd term of the arithmetic sequence

Answer 1

ans: B: 31/4 is the 103rd term of the arithmetic sequence

Answer 2

option B: 31/4

Explanation:

Given

-3/4, -2/3 , -7/12, -1/2...........

General formula for arithmeti sequence to find nth term is

a_n = a_1 + (n-1) d

first term a_1 = -3/4

We find out common difference 'd'

Lets find the difference of first two terms

`(-2)/(3) -(-3)/(4) = (-8)/(12) +(9)/(12) =(1)/(12)`

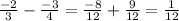
common difference is 1/12

now we need to find 103rd term

`a_n = a_1 + (n-1) d`

First term is -3/4, d= 1/12

`a_(103) = (-3)/(4)+(103-1)(1)/(12)`

`a_(103) = (-3)/(4)+(102)(1)/(12)`

`a_(103) = (-3)/(4)+(34)/(4)`

`a_(103) = (-3+34)/(4)`

`a_(103) = (31)/(4)`