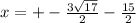Question

By completing the square. What is the missing term required to
form a square trinomial?

Answer 1

Missing term is 225/4

Explanation:

`x^2+15x+18=0`

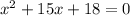
First move +18 to the other side. Subtract 18 on both sides

`x^2+15x=-18`

In completing the square method we take the half of coefficient of x and then square it

coefficient of x is 15

Half of 15 is
`(15)/(2)`

Square it
`((15)/(2))^2`

`(225)/(4)`

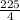
Missing term is 225/4 that is required to form a square trinomial

Add it on both sides

`x^2+15x+(225)/(4)=-18+(225)/(4)`

`x^2+15x+(225)/(4)=(-18*4)/(1*4)+(225)/(4)`

`x^2+15x+(225)/(4)=(-72)/(4)+(225)/(4)`

`x^2+15x+(225)/(4)=(153)/(4)`

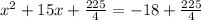
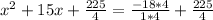
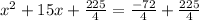
Now we write left hand side in square form

`(x+(15)/(2))^2=(153)/(4)`

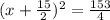
Now we solve for x

Take square root on both sides

`(x+(15)/(2))^2=\sqrt{(153)/(4)}`

`(x+(15)/(2))=+-(3√(17))/(2)`

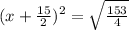
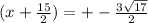
Subtract 15/2 on both sides

`x=+-(3√(17))/(2)-(15)/(2)`