Question

A carbon steel helical compression spring with squared and ground ends has an outside diameter of 0.85 in and a wire diameter of 0.074 in. The free length is 2 in, and the solid length is 0.618 in. Find the spring constant and the load required to compress the spring to the solid length.\

Answer 1

Given :

d = diameter of the wire of the spring = 0.074 in

= 0.188 cm

R = mean radius of coil
`$=(0.85)/(2)$`

= 1.08 cm

G = modulus of rigidity of carbon steel wire =
`$79 \ GN/m^2$`

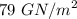
L = length of wire of spring = 2 inch

∴ L = 5.08 cm

k = spring constant

k = axial load/ axial deflection

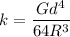`$k= (Gd^4)/(64R^3)$` ..................(1)

This is taken from the Torsion equation,

`$(T)/(I_P)=(\tau_(max))/(d/2)=(G \theta)/(2 \pi R)$`

`$(WR)/((\pi)/(32) d^4) = (\tau_(max))/(d/2) =(G \theta)/(2 \pi R)$`

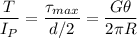
∴ From equation (1)

`$k =(79 * 10^9 * (0.188)^4 * 10^(-8))/(64 * (1.08)^3 * 10^(-6))$`

`$k = 11334 \ N/m $`

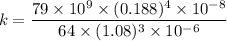
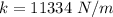
So the axial compression is
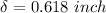`$ \delta =0.618 \ inch$` = 1.57 cm

Axial load required W= k x δ

= 11334 x 1.57

= 177.95 N