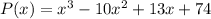Answer:
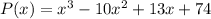
Step-by-step explanation: We are given roots of a third degree polynomial function -2, 6+i.
Note: a radical always comes with pair of plus and minus sign.
Therefore, there would be one more root 6-i.
So, all the roots would be -2, 6+i, 6-i.
So, the factors of polynomial function would be
(x+2)(x-6-i)(x-6+i)
Multiplying those factors,
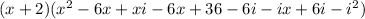
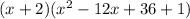
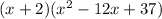
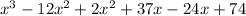
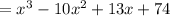
Therefore,