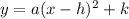Question

What is the equation of the quadratic graph with a focus of (1, -3) and a directrix of y= -1 ? Show work

hint: y=a(x-h)^2+k, a=1/4
(x-x1)^2+ 9y-y1)^2= (y-y2)^2

Answer 1

`y=(-1)/(4)(x-1)^2-2`

Explanation:

Given : focus of (1, -3) and a directrix of y= -1

The distance between focus and directrix is 2p

The distance between (1,-3) and y=-1 is 2

So 2p = 2 and p =1

Vertex (h,k) lies inbetween the focus and directrix

focus is (h, k-p)

given focus is (1,-3)

so h=1 and k-p = -3 ( we got p =1)

So k-1= -3 , k= -2

Hence, vertex is (1,-2), h=1 and k = -2

`a=(1)/(4p) =(1)/(4)`

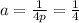
Here focus at the bottom and directrix at the top

so parabola opens down

hence a= -1/4

Plug it in the equation

`y=a(x-h)^2+k`

`y=(-1)/(4)(x-1)^2-2`