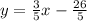Question

Indicate the equation of the line that is the perpendicular bisector of the segment with endpoints (4, 1) and (2, -5).

Indicate the equation of the line through (2, -4) and having slope of 3/5.

Answer 1

Explanation:

y = mx + b.....the m is for the slope , (2,-4)...x = 2 and y = -4

now we sub

-4 = 3/5(2) + b

-4 = 6/5 + b

-4 - 6/5 = b

-20/5 - 6/5 = b

- 26/5 = b

so ur equation is : y = 3/5x - 26/5 <== slope intercept form

or if u need it in standard form :

y = 3/5x - 26/5....(5)

5y = 3x - 26

-3x + 5y = -26...(-1)

3x - 5y = 26 <==standard form

Answer 2

Given endpoint are (4,1) and (2, -5).

For any two points
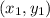`(x_1 , y_1)` and
`(x_2 , y_2)`

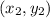
Slope of the line is given by:

Slope(m) =
`(y_2-y_1)/(x_2-x_1)`

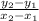
Slope of the segment for the given end points are:

`m_1= (-5-1)/(4-2) =(-6)/(2) = -3`

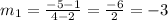
Now, to find the midpoint of line segment.

Midpoint is halfway between the two end points.

then its y value is halfway between the two y values and Its x value is halfway between the two x values.

i.e,

Midpoint =
`((x_1+x_2)/(2) , (y_1+y_2)/(2) )`

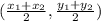
Midpoint of the given line segment is;

`((4+2)/(2) , (1-5)/(2) ) = ((6)/(2) , (-4)/(2)) = (3, -2)`

we have to find the equation of line that is perpendicular bisector of the line segment.

Slope for the perpendicular bisector
`m_2` ;

`m_1 * m_2 = -1`

`-3 * m_2 = -1`

⇒
`m_2 = (1)/(3)`

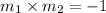
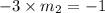
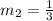
Point slope form: An equation of a straight line in the form
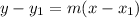`y-y_1 = m(x -x_1)` where m is the slope of the line and
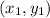`(x_1, y_1)` are the coordinates of a given points on the line

Using point slope form to find the equation of line that is the perpendicular bisector;

`y - (-2) = (1)/(3)(x-3)`

`y+2 = (1)/(3)(x-3)`

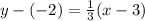
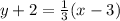
Using distributive property;

`y +2 =(1)/(3) x -1`

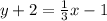
or

`y = (1)/(3) x -1-2`

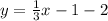
or

`y = (1)/(3) x - 3`

Therefore, the equation of line that is perpendicular bisector of the segment with given end points is;
`y = (1)/(3) x - 3`

To indicate the equation of line through (2, -4) and having slope of
`(3)/(5)`

Using Point slope form definition :

`y-y_1 = m(x-x_1)`

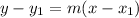
then;

`y-(-4)=(3)/(5) (x-2)`

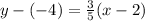
or

`y+4 = (3)/(5) (x-2)`

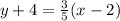
Using distributive property:

`y+4 = (3)/(5)x-(6)/(5)`

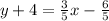
Subtract 4 from both sides we get;

`y = (3)/(5)x-(6)/(5) -4`

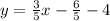
or

`y = (3)/(5)x-(26)/(5)`

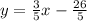
therefore, the equation of line is ,
`y = (3)/(5)x-(26)/(5)`