Answer: The solutions are :
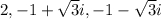
Our equation is
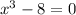
and we know that:
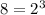
then we can write our equation as:
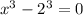
And using the identity:
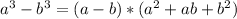
where a = x and b = 2, then our equation is:
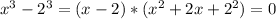
them, if x = 2 the first part is zero, so x = 2 is a solution, and now we need to see the second part in order to find the complex solutions.
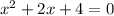
Here we need to use Bhaskara:
if
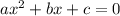 for a, b and c constants, then:
for a, b and c constants, then:
x =
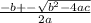
in our problem we have:
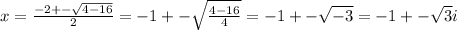
So here we have two complex solutions:
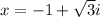 and
and
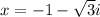 .
.