Question

Three charges, each separated by 100 m from adjacent charges, are located along a horizontal line: a -3.00 C charge on the left, a 2.00 C charge in the middle, and a 1.00 C charge on the right. What is the resultant force on the 1.00 C charge due to the other two

Answer 1

F= 11.25*10⁵ N to the right.

Step-by-step explanation:

• Assuming that the three charges can be treated like point charges, they must obey Coulomb's Law.
• Due to the linearity of this Law, we can use superposition in order to find the resultant force on the 1.00 C charge due to the other two.
• First, we find the force that the -3.00 C charge (located 200 m to the left) exerts on the 1.00 C, as follows:

`F_(13) = (K*q_(1)*q_(2))/(r_(13) ^(2) ) = (9e9*(-3.00C)(1.00C))/((200m)^(2)) = -6.75e5 N (1)`

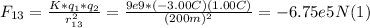
• Then, in the same way, we can find the force that the 2.00 C exerts on the 1.00 C charge, located 100 m away to the left:

`F_(23) = (K*q_(3)*q_(2))/(r_(23) ^(2) ) = (9e9*(2.00C)(1.00C))/((100m)^(2)) = 18e5 N (2)`

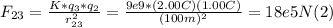
• Since both vectors are on the same line, their sum is directly the algebraic sum, as follows:
• F₃ = F₁₃ + F₂₃ = -6.75*10⁵ N + 18.00*10⁵ N = 11.25*10⁵ N to the right, assuming this direction as positive.