Question

from right circular cylinder with height 10 cm and radius of base 6 CM a right circular cone of the same height and base is remote find the volume of the remaining solid

Answer 1

753.98 cubic cm.

Explanation:

We have been given that from right circular cylinder with height 10 cm and radius of base 6 cm, a right circular cone of the same height and base is removed.

To find the area of remaining solid we will subtract volume of cone from volume of cylinder.

`\text{Volume of remaining solid}=\text{Volume of cylinder- Volume of cone}`

`\text{Volume of remaining solid}=\pi r^(2) h- (1)/(3)\pi r^(2)h`

`\text{Volume of remaining solid}=(3)/(3)\pi r^(2) h- (1)/(3)\pi r^(2)h`

`\text{Volume of remaining solid}=(2)/(3)\pi r^(2) h`

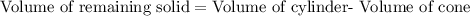
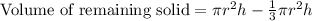
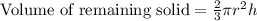
Upon substituting our given values in the formula we will get,

`\text{Volume of remaining solid}=(2)/(3)\pi*6^(2)*10`

`\text{Volume of remaining solid}=(2)/(3)\pi*36*10`

`\text{Volume of remaining solid}=2*\pi*12*10`

`\text{Volume of remaining solid}=240\pi`

`\text{Volume of remaining solid}=753.9822368615503772\approx 753.98`

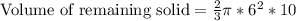
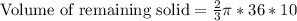
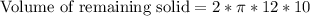
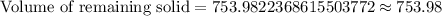
Therefore, the volume of remaining solid is 753.98 cubic cm.