Question

Please help!

Which inequality matches the graph?
(See photo)

A. −2x + 3y > 7
B. 2x − 3y < 7
C. −3x + 2y ≥ 7
D. 3x − 2y ≤ 7

Answer 1

To find which inequality matches the graph, we will first look at the graph.

As, by looking at the graph, i observe that, the line passes through (5,1) and (-5,-4).

Equation of line passing through two points
`(x_(1),y_(1)) {\text{and}} (x_(2),y_(2)) is =((y_(2)-y_(1)))/((x_(2)-x_(1)))`.

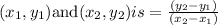So, equation of line passing through (5,1) and (-5,-4) is ,

`(y-1)/(x-5)=(1+4)/(5+5)\\\\ 2 y -2=x-5\\\\ x -2 y+2-5=0\\\\ x - 2 y-3=0`

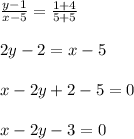
Putting , x=0 and y=0 in above equation of line, I get negative value, which shows point is contained inside the region of the inequality,

→x-2 y≤ 3, as this inequality is not among given options, so by taking intercept form of line,

`(x)/(3.2)+(y)/(-2.3)\leq 1{\text{As slope intercept form of line is}}, (x)/(a)+(y)/(b)=1\\\\ 2.3 x-3.2 y\leq 2.3 * 3.2 \\\\ 2.3 x-3.2 y\leq 7.36`

Which can be written as, 2 x -3 y< 7

Option (B) →2 x − 3 y < 7, is the appropriate inequality among four options which matches the graph .

Answer 2

Option B is correct.

Explanation:

We have been given four inequalities and a graph we need to tell which one of these inequalities matches the graph.

So, the graph of each inequality is attached in the attachment.

Graphs attached in sequence of the inequality.

Therefore, Option B is correct.