Question

Question 1

Expand (x - 2)6.

x6 + 12x5 + 60x4 + 160x3 + 240x2 + 192x + 64

x6 - 12x5 - 60x4 - 160x3 - 240x2 - 192x - 64

x6 - 12x5 + 60x4 - 160x3 + 240x2 - 192x + 64

x6 - 12x5 + 60x4 - 160x3 + 240x2 - 160x + 64

2 points
Question 2

Expand (x + 2y)4.

x4 - 8x3y + 24x2y2 - 32xy3 + 16y4

x4 + 8x3y + 24x2y2 + 32xy3 + 16y4

x4 + 8x3y + 28x2y2 + 32xy3 + 16y4

x4 + 8x3y + 24x2y2 + 34xy3 + 16y4

2 points
Question 3

How many terms are in the expansion (a + b)20.

19

20

21

22

2 points
Question 4

Expand (x - y)4.

x4 - 5x3y + 6x2y2 - 5xy3 + y4

x4 - 4x3y + 8x2y2 - 4xy3 + y4

x4 - 4x3y + 6x2y2 - 4xy3 + y4

x4 - 4x3y + 6x2y2 - 4xy3 - y4

2 points
Question 5

Expand (5a + b)5.

295a5 + 3125a4b + 1250a3b2 + 250a2b3 + 25ab4 + b5

3125a5 + 3125a4b + 1250a3b2 + 250a2b3 + 25ab4 + b5

3125a5 - 3125a4b + 1250a3b2 - 250a2b3 + 25ab4 - b5

3125a5 + 3125a4b + 1250a3b2 + 250a2b3 + 25ab4 + 10b5

2 points
Question 6

Expand (x + 2y)5.

x5 + 10x4y + 40x3y2 + 80x2y3 + 80xy4 + 32y5

x5 - 10x4y + 40x3y2 - 80x2y3 + 80xy4 - 32y5

x5 - 10x4y + 40x3y2 - 80x2y3 + 80xy4 - 32y5

x5 - 10x4y + 40x3y2 - 80x2y3 + 80xy4 - 32y5

2 points
Question 7

What is the sixth term of (a - y)7?

21a3y4

-21a3y4

21a2y5

-21a2y5

2 points
Question 8

What is the 6th term of (2x - 3y)11?

7,187,024x6y5

-7,185,024x6y5

7,185,024x6y5

-7,187,024x6y5

2 points
Question 9

What is the sixth term of (x + y)8?

56x3y5

36x3y5

36x4y4

56x4y4

2 points
Question 10

What is the seventh terms of (x + 4)8?

114,688x2

114,688x3

114,688x4

114,688x5

Answer 1

QUESTION 1

We want to expand
`(x-2)^6`.

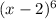We apply the binomial theorem which is given by the formula

`(a+b)^n=^nC_0a^nb^0+^nC_1a^(n-1)b^1+^nC_2a^(n-2)b^2+...+^nC_na^(n-n)b^n`.

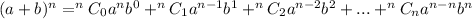By comparison,

`a=x,b=-2,n=6`.

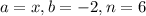We substitute all these values to obtain,

`(x-2)^6=^6C_0x^6(-2)^0+^6C_1x^(6-1)(-2)^1+^6C_2x^(6-2)(-2)^2+^6C_3x^(6-3)(-2)^3+^6C_4x^(6-4)(-2)^4+^6C_5x^(6-5)(-2)^5+^6C_6x^(6-6)(-2)^6`.

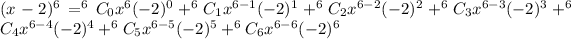We now simplify to obtain,

`(x-2)^6=^nC_0x^6(-2)^0+^6C_1x^(5)(-2)^1+^6C_2x^(4)(-2)^2+^6C_3x^(3)(-2)^3+^6C_4x^(2)(-2)^4+^6C_5x^(1)(-2)^5+^6C_6x^(0)(-2)^6`.

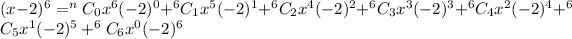This gives,

`(x-2)^6=x^6-12x^(5)+60x^(4)-160x^(3)(-2)^3+240x^(2)-1925x+64`.

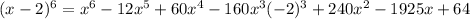Ans:C

QUESTION 2

We want to expand

`(x+2y)^4`.

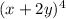We apply the binomial theorem to obtain,

`(x+2y)^4=^4C_0x^4(2y)^0+^4C_1x^(4-1)(2y)^1+^4C_2x^(4-2)(2y)^2+^4C_3x^(4-3)(2y)^3+^4C_4x^(4-4)(2y)^4`.

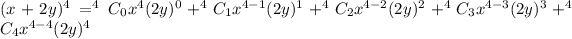We simplify to get,

`(x+2y)^4=x^4(2y)^0+4x^(3)(2y)^1+6x^(2)(2y)^2+4x^(1)(2y)^3+x^(0)(2y)^4`.

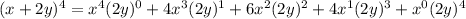We simplify further to obtain,

`(x+2y)^4=x^4+8x^(3)y+24x^(2)y^2+32x^(1)y^3+16y^4`

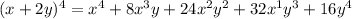
Ans:B

QUESTION 3

We want to find the number of terms in the binomial expansion,

`(a+b)^(20)`.

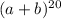In the above expression,
`n=20`.

The number of terms in a binomial expression is
`(n+1)=20+1=21`.

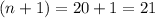Therefore there are 21 terms in the binomial expansion.

Ans:C

QUESTION 4

We want to expand

`(x-y)^4`.

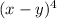We apply the binomial theorem to obtain,

`(x-y)^4=^4C_0x^4(-y)^0+^4C_1x^(4-1)(-y)^1+^4C_2x^(4-2)(2y)^2+^4C_3x^(4-3)(-y)^3+^4C_4x^(4-4)(-y)^4`.

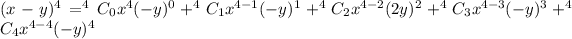We simplify to get,

`(x+2y)^4=^x^4(-y)^0+4x^(3)(-y)^1+6x^(2)(-y)^2+4x^(1)(-y)^3+x^(0)(-y)^4`.

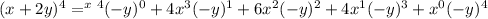We simplify further to obtain,

`(x+2y)^4=x^4-4x^(3)y+6x^(2)y^2-4x^(1)y^3+y^4`

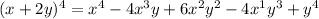
Ans: C

QUESTION 5

We want to expand
`(5a+b)^5`

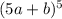
We apply the binomial theorem to obtain,

`(5a+b)^5=^5C_0(5a)^5(b)^0+^5C_1(5a)^(5-1)(b)^1+^5C_2(5a)^(5-2)(b)^2+^5C_3(5a)^(5-3)(b)^3+^5C_4(5a)^(5-4)(b)^4+^5C_5(5a)^(5-5)(b)^5`.

We simplify to obtain,

`(5a+b)^5=^5C_0(5a)^5(b)^0+^5C_1(5a)^(4)(b)^1+^5C_2(5a)^(3)(b)^2+^5C_3(5a)^(2)(b)^3+^5C_4(5a)^(1)(b)^4+^5C_5(5a)^(0)(b)^5`.

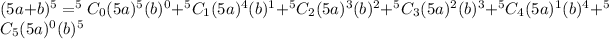This finally gives us,

`(5a+b)^5=3125a^5+3125a^(4)b+1250a^(3)b^2+^250a^(2)(b)^3+25a(b)^4+b^5`.

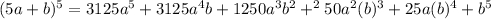Ans:B

QUESTION 6

We want to expand
`(x+2y)^5`.

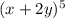We apply the binomial theorem to obtain,

`(x+2y)^5=^5C_0(x)^5(2y)^0+^5C_1(x)^(5-1)(2y)^1+^5C_2(x)^(5-2)(2y)^2+^5C_3(x)^(5-3)(2y)^3+^5C_4(x)^(5-4)(2y)^4+^5C_5(x)^(5-5)(2y)^5`.

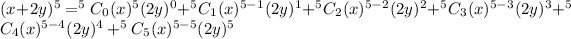We simplify to get,

`(x+2y)^5=^5C_0(x)^5(2y)^0+^5C_1(x)^(4)(2y)^1+^5C_2(x)^(3)(2y)^2+^5C_3(x)^(2)(2y)^3+^5C_4(x)^(1)(2y)^4+^5C_5(x)^(0)(2y)^5`.

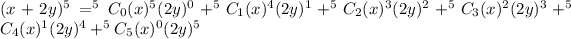This will give us,

`(x+2y)^5=x^5+^10(x)^(4)y+40(x)^(3)y^2+80(x)^(2)y^3+80(x)y^4+32y^5`.

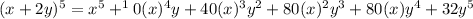Ans:A

QUESTION 7

We want to find the 6th term of
`(a-y)^7`.

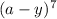The nth term is given by the formula,

`T_(r+1)=^nC_ra^(n-r)b^r`.

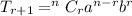Where
`r=5,n=7,b=-y`

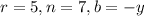
We substitute to obtain,

`T_(5+1)=^7C_5a^(7-5)(-y)^5`.

`T_(6)=-21a^(2)y^5`.

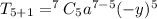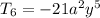Ans:D

QUESTION 8.

We want to find the 6th term of
`(2x-3y)^(11)`

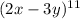
The nth term is given by the formula,

`T_(r+1)=^nC_ra^(n-r)b^r`.

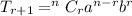Where
`r=5,n=11,a=2x,b=-3y`

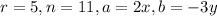
We substitute to obtain,

`T_(5+1)=^(11)C_5(2x)^(11-5)(-3y)^5`.

`T_(6)=-7,185,024x^(6)y^5`.

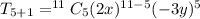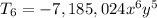Ans:D

QUESTION 9

We want to find the 6th term of
`(x+y)^8`.

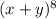The nth term is given by the formula,

`T_(r+1)=^nC_ra^(n-r)b^r`.

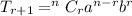Where
`r=5,n=8,a=x,b=y`

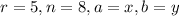
We substitute to obtain,

`T_(5+1)=^8C_5(x)^(8-5)(y)^5`.

`T_(6)=56a^(3)y^5`.

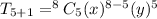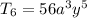Ans: A

We want to find the 7th term of
`(x+4)^8`.

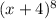The nth term is given by the formula,

`T_(r+1)=^nC_ra^(n-r)b^r`.

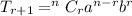Where
`r=6,n=8,a=x,b=4`

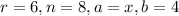
We substitute to obtain,

`T_(6+1)=^8C_5(x)^(8-6)(4)^6`.

`T_(7)=114688x^(2)`.

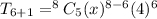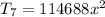Ans:A