Question

Hard question but would help me out

Answer 1

Critical value f(1)=2.

Minimum at (1,2), function is decreasing for
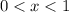`0<x<1` and increasing for
`x>1.`

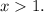
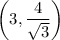`\left(3,(4)/(√(3))\right)` is point of inflection.

When 0<x<3, function is concave upwards and when x>3, , function is concave downwards.

Explanation:

1. Find the domain of the function f(x):

`\left\{\begin{array}{l}x\ge 0\\x\\eq 0\end{array}\right.\Rightarrow x>0.`

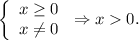
2. Find the derivative f'(x):

`f'(x)=((x+1)'\cdot √(x)-(x+1)\cdot (√(x))')/((√(x))^2)=(√(x)-(x+1)/(2√(x)))/(x)=(2x-x-1)/(2x√(x))=\frac{x-1}{2x^{(3)/(2)}}.`

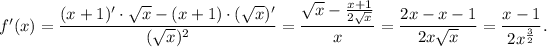
This derivative is equal to 0 at x=1 and is not defined at x=0. Since x=0 is not a point from the domain, the crititcal point is only x=1. The critical value is

`f(1)=(1+1)/(√(1))=2.`

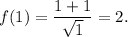
2. For
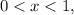`0<x<1,` the derivative f'(x)<0, then the function is decreasing. For
`x>1,` the derivative f'(x)>0, then the function is increasing. This means that point x=1 is point of minimum.

3. Find f''(x):

`f''(x)=\frac{(x-1)'\cdot 2x^{(3)/(2)}-(x-1)\cdot (2x^{(3)/(2)})'}{(2x^{(3)/(2)})^2}=`

`=\frac{2x^{(3)/(2)}-2(x-1)\cdot (3)/(2)x^{(1)/(2)}}{4x^3}=\frac{2x^{(3)/(2)}-2\cdot(3)/(2)x^{(3)/(2)}+ 2\cdot(3)/(2)x^{(1)/(2)}}{4x^3}=`

`=\frac{-x+3}{4x^{(5)/(2)}}.`

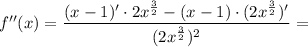
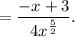
When f''(x)=0, x=3 and
`f(3)=(3+1)/(√(3))=(4)/(√(3)).`

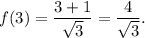
When 0<x<3, f''(x)>0 - function is concave upwards and when x>3, f''(x)>0 - function is concave downwards.

Point
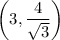`\left(3,(4)/(√(3))\right)` is point of inflection.