Answer:
The second base 375 feet away from the outfielder.
Explanation:
The given equation is
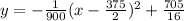
Where y is the height of the ball in feet after the ball has traveled x feet horizontally.
Put x=0, to find the initial height of the bal.
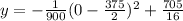
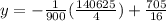
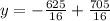

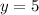
Therefore the initial height of the ball is 5 feet.
The second baseman catches the ball at the same height as the height at which the outfielder released it.
Put y=5 at find the another value of x, for which the height of the ball is 5.
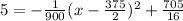

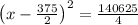
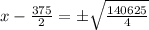
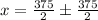
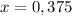
Therefore the second value of x is 375 for which the height of ball is 5.
Therefore the second base 375 feet away from the outfielder.