Question

Given: KPST is a trapezoid, KP=ST,

MN is a midsegment
MN=20,
h=15, PS:KT=3:7
Find: KS and KP

Answer 1

Length of KS and KP are; 25 and 17

Explanation:

Given: KPST is a trapezoid, KP =ST, MN is a mid segment, h is the height =15

Also, MN = 20 , h = 15 and PS:KT = 3:7.

• If two sides of the trapezoid are equal then, it is an isosceles trapezoid.

• Mid-segment of a trapezoid is a line segment which connects the midpoints of the non-parallel sides.
• A trapezoid mid segment connects the midpoints of two congruent sides of the trapezoid and is parallel to the pair of parallel sides.
• Length of the mid segment is the sum of two bases divide by 2

Since, the length of Mid-segment MN = 20.

Also, it is given: PS:KT = 3:7

Let bases PS = 3x and KT = 7x respectively.

then;

`(PS+KT)/(2) = 20`

`(3x+7x)/(2) = 20`

`(10x)/(2) = 20`

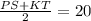
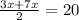
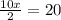
Simplify:

5x =20

Divide both sides by 5 we get;

x =4

Then:

Length of base PS = 3x = 3(4) = 12

and Length of base KT = 7x = 7(4) = 28.

In triangle PLK

Using Pythagoras theorem to find KP;

here, PL =h =15 and KL= 8 {you can see in the figure as shown below};

`KP^2 = PL^2+KL^2`

`KP^2 = 15^2+8^2 = 225+64 = 289`

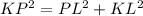
or

`KP = √(289) = 17`

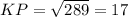
therefore, the length KP = 17

Construct a line: Join K and S

Now, in triangle KRS

KR = KL+LR = 8+12 = 20 and SR = h= 15

Using Pythagoras theorem in KRS to find KS ,

`KS^2 = SR^2+KR^2`

`KS^2 = 15^2+20^2 = 225+400 = 625`

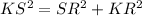
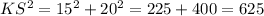
or

`KS = √(625) = 25`

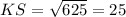
Therefore, the length of KS is, 25